ここでは、三角関数などを必要とする計算を行います。高校で学ぶ数学の知識が必要です。
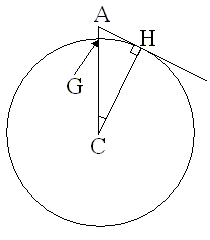
上の図を見てください。
ものすごく簡単な模式図ですが、Gという点に立っている人が見る地平線を考えてみました。Aは、視点の位置です。また、C点は月の中心です。
地平線というのは、視線が地球や月の表面に接する点と考えられます。従って、上の図では、視線と月面とが接する点Hが地平線としてみえている場所と考えられます。
また、自分が今いる場所から地平線までの距離は、上の図でいいますと弧GHになります。
簡単のために、ここでは月は球であると考えましょう。また、起伏についても今は考えないでおきます。
また、月の半径(距離CG。約1738km)に比べますと、視野の高さ(距離AG。せいぜい1.6m)は非常に小さい数値です(上の図は極端に誇張して書かれていることにご注意下さい)。
では、弧GHの長さを求めてみることにしましょう。
角GCHをθ(シータ)、月の半径を r としましょう。また、角度を「ラジアン」(平面角。弧の長さと半径の比)で表すことにします。そうしますと、弧GHはrθで表されます。
一方、θは三角関数のcos(コサイン)を使って、
cos θ = r / AC
と表されます。
ここからは、逆三角関数を使うシンプルなやり方と、cos θをそのまま使って近似的に解く導き方の2種類の解き方で進んでみましょう。
■ 逆三角関数を使って計算する場合
θ = cos-1 ( r / AC )
ACは、月の半径(GC)に視点の高さ(AG)を加えたものです。つまり、1738km+1.6m ということになります(単位に注意してください)。 r に1738km、ACを1738.0016km を代入しますと、
r / AC = 1738 [km] / 1738.0016 [km] = 0.99999907940245854779420226080344
となります(小数点の下の部分を長々と書いても、実際には有効数字の問題がありますので意味はありません)。
この値からθを求めますと、
θ=cos-1 0.99999907940245854779420226080344
=0.07774513979 [度]
=0.00135690866 [ラジアン]
となります。ものすごく小さな角度であることはお分かりいただけますでしょうか。
これをもとに rθを計算してみますと、
1738 [km] × 0.00135690866 [ラジアン] = 約 2.358 [km]
■ cos θをそのまま使う場合
求めたいのは弧GHの長さですが、いま、θは極めて小さい角度なので、弧GHの長さは、直線AHの長さとほとんど同じと考えられます。
このAHの長さは、
AH = r sin θ
で表されます。 ところで、
cos2 θ + sin2 θ = 1
ですから、
sin θ = √( 1 − cos2 θ )
となります。この sin θの式を使うと、
AH = r × √ { 1 − ( r / AC )2 }
値を代入して計算すると、
AH = 1738 [km] × √{ 1 − ( 1738 [km] / 1738.0016 [km] )2 }
= 2.358 [km]
となります。上の逆三角関数を使う方法とほとんど違わない結果になっています。
以上、2種類の回答を示しました。いずれにしても、意外に思われるかもしれませんが、月の地平線は、これほどの距離しか離れていないのです。
ちなみに、地球上で地平線の距離はどうなるでしょうか? これは、rを地球の半径(6378km)として計算をしてみればよいことになります。計算の過程は省略しますが、結果は、約4.5kmとなります。地平線や水平線は遠くにあるのだと思っていらした方、意外に近い距離でびっくりされたのではないでしょうか。
もし皆様のお手許に関数電卓などがありましたら、ぜひ一度計算してみてください。
